Ha meg akarunk tanítani valamit egy gyermeknek, akkor valamennyit értenünk kell a dolog lényegéhez, nehogy a tanítás és a nevelés során olyan dolgok között mozogjunk, amelyek távol állnak az élettől. Mindent, ami közel áll az élethez, meg lehet érteni. Úgy is mondhatnánk: amit valóban megértünk, annak közel kell állnia az élethez. Az absztrakciók nem állnak közel az élethez.

Manapság az a helyzet, hogy a tanárnak, nevelőnek bizonyos dolgokról kezdettől fogva csak absztrakciói vannak; mert ezek nem állnak közel az élethez. Ez a lehető legnagyobb nehézségeket idézi elő a nevelés és a tanítás során. Gondolják csak végig a következőt: gondolkozzanak azon, hogyan is jutottak oda, hogy megszámoljanak dolgokat; hogy mit is tesznek, amikor számolnak. Valószínűleg azt fogják találni, hogy a vizsgálódásaik fonala valahol megszakad, hogy bizonyára megtanultak számolni, de nem igazán tudják, mit is tesznek számoláskor.

Nos, a pedagógiában mindenféle elméleteket okoskodnak ki arról, hogyan is kell megtanítani a gyermeknek a számfogalmat, a számolást, és rendszerint az ember igazodik is ezekhez az elméletekhez. Ha külsőleg siker érhető is el így, a teljes emberhez nem kerülünk közel az efféle számolással, illetve olyan dolgokkal, amelyek távol állnak az élettől. Az újabb korunk éppen azzal bizonyította be, hogy mennyire absztrakciókban él, hogy olyan dolgokat talált ki a tanítás számára, mint a számológép. A kereskedelmi irodákban használjanak csak számológépet az emberek, ahogy tetszik nekik, ezzel most nem foglalkozunk, a tanításban azonban a számológép, amely kizárólag a fejhez szól, kezdettől fogva meggátolja, hogy lényegszerűen vigyük közel a gyermekhez a számot.

Arról van szó, hogy valóban az életből vezessük le a számolást. Ennél mindenekelőtt az a fontos, hogy kezdettől tudjuk, egyáltalán nem is lehet lényeges, hogy a gyermek maradéktalanul megértsen mindent, amit tanítunk neki. A gyereknek sok mindent az autoritásból fakadóan kell befogadnia, de természetes, tárgyilagos módon kell befogadnia.

Ezért bizony úgy találhatják, hogy amit most elmondok majd önöknek a számolás tanításáról, talán nehéz még a gyermeknek. Ez azonban egyáltalán nem árt. Rendkívüli jelentősége van annak, hogy az ember életében elkövetkezzenek olyan pillanatok, amikor a harmincadik, a negyvenedik életévében járva azt mondja magában: most értem meg, amit annak idején 8 vagy 9 évesen, vagy talán még korábban, az autoritásból fakadóan fogadtam be... Ez élettel telít. Aki viszont azokra a dolgokra tekint, amiket ezzel szemben manapság szemléltető oktatásként akarnak bevezetni a tanításba, az tényleg kétségbe eshet, hogy milyen triviálissá teszik is a dolgokat, hogy - amint mondják - közelebb hozzák azokat a gyermek értelmi szintjéhez.

Képzeljék csak el, hogy vesszük akár a legkisebb gyermeket, aki még igen ügyetlen e téren, és azt mondjuk neki: nézd csak, a- hogy most itt állsz. Fogok egy fadarabot. Itt egy kés. Most felvagdalom vele ezt a fadarabot. Megtehetném ezt veled is? Akkor ugye a gyerek magától rájön, hogy vele nem tehetném meg ezt. És most azt mondhatjuk a gyereknek: látod, ha a fadarabot fel tudom vagdalni, akkor ugye a fa nem olyan, mint te vagy, hiszen téged nem darabolhatnálak fel. Különbség van tehát közted és a fa között. Az a különbség, hogy te egység vagy. A fadarab nem egység. Te egység vagy. Téged nem darabolhatnálak fel. Azt, ami te vagy, mert téged nem tudlak feldarabolni, egységnek nevezem.

Most pedig fokozatosan rátérünk arra, hogy egy jelet adjunk a gyereknek ezen egység számára. Egy vonalat húzunk: 1.’ Megtanítjuk tehát a gyereknek, hogy ez egy egység, és ilyen vonalat húzunk a jelölésére.

Majd eltávolodhatunk a fadarabtól és a gyermekkel való összehasonlítástól, és most azt mondhatjuk a gyereknek: nézd csak, van egy jobb kezed, és van egy bal kezed is. És megtaníthatjuk neki: ha csak ez az egy kezed volna, akkor ez az egy kezed mindenfelé tudna mozdulni, ahol te magad vagy. De ha így jársz-kelsz, akkor nem találkozhatsz magaddal, nem érintkezhetsz önmagaddal. Ha viszont ez a kezed és a másik kezed is mozdul, akkor összeérhetnek, találkozhatnak. Ez más, mint ahogy te csak egymagad jársz-kelsz. Mert te egymagad jársz, egy egység vagy. Az egyik kezed viszont találkozhat a másik kezeddel. Ez már nem egység, hanem kettősség. Látod, te magad egy vagy, de két kezed van. Ezt ezután így jelölöd: 11.

Ily módon az egység és kettősség fogalmát magából a gyermekből kiindulva hozzuk létre.

Most megint tovább lépünk, kiszólítunk egy második gyermeket is, és azt mondjuk: ha viszont ti ketten jártok-keltek, ti is összetalálkozhattok, ti is érintkezhettek. Ti együtt kettősséget alkottok. És még valaki csatlakozhat hozzátok. A kezeitekkel ez nem történhet meg. Így rátérhetünk a gyermekkel a hármasságra: 111.

Így lehet abból, ami az ember saját maga, levezetnünk a számokat: az embertől jutunk a számokhoz. Az ember eleven, nem absztrakció.

És tovább is mehetünk, és azt mondhatjuk: figyelj csak, másutt is van még rajtad egy másik kettősség... Addig vezetjük, amíg eljut a gyermek a lábaihoz. Akkor azt mondjuk: de ugye láttad már a szomszédék kutyáját, az is csak két lábon jár? S akkor eljut a gyermek oda, hogy a négy vonásban 1111 felismeri a szomszédék kutyájának a járását, és így fokozatosan az életből kiindulva tanulja meg felépíteni a számokat.

Bizony jó, ha a tanár mindenütt nyitott szemmel jár, és mindenre értőn tekint. Így a gyermeket például igen jól rávezethetjük, mert így előbb, amint ez természetes, ezeket az úgynevezett római számokat újuk - hiszen ez az, amit a gyermek magától értetődően mindjárt felfog - a négyről az ötre való, átmenetre: V. Azt mondjuk ekkor a gyereknek: látod, ha ezt az ujjadat (a hüvelykujját) a tenyeredbe hajtod, akkor ezt a négyet úgy használhatod, mint a kutya: 1111. Akkor azután hozzájön még a hüvelykujjad is, most már öten vannak: V.

Láttam egyszer egy tanárt, aki a római számok elmagyará- zásában eljutott négyig, de nem tudott rájönni, miért nem az jutott a rómaiak eszébe, hogy azután öt vonást húzzanak egymás mellé, hanem ezt a V-jelet adták az ötnek. A 1 111 jelölésig egész jól haladt előre. Azt mondtam akkor: csináljunk most úgy, hogy kétfelé bontva tárjuk szét az öt ujjunkat, és máris itt van - így van benne, a római ötösben, a kéz. Így is keletkezett a római ötös. A kéz rejlik benne.

Egy ilyen rövid kurzusban természetesen csak az elvet tudjuk bemutatni. De ezen a módon lehetőségünk nyílik arra, hogy magukat a számokat közvetlenül az életből tudjuk kiolvasni. És csak azután, hogy ily módon közvetlenül az életből bontottuk ki a számokat, próbáljuk meg a számok egymás utáni sorba állításával bevezetni a számolást. De próbáljuk meg úgy átvenni ezt, hogy ne legyen semleges élmény a gyerekek számára. Mielőtt azt mondanánk: sorold csak el nekem egymás után a számokat - 1, 2, 3, 4, 5, 6, 7, 8, 9 stb., előbb a ritmusból induljunk ki. Mondjuk, hogy egyről kettőre lépünk: 1-2, 1-2, 1-2; erősebben lépjen a gyerek a lábára a 2-nél, és a 3-ra is így ritmikusan térünk át: 1-2-3, 1-2-3. Ily módon ritmust viszünk a számsorba, és azt a képességet is fejlesztjük a gyermekben, hogy csoportosítsa a dolgokat. Így valóban természetes módon jutunk el oda, hogy a számok lényegéből, lényéből kiindulva tanítsuk meg a gyereknek a számokat.

Az ember rendszerint azt hiszi, ő találta ki a számokat, ahogy mindig hozzátett egyet a többihez. Ez azonban egyáltalán nem igaz, a fejünk egyáltalán nem számol. A mindennapi életben nem is hisszük, micsoda egy különös, haszontalan szerv is tulajdonképpen ez az emberi fej a földi lét számára. A szépségéért van ott, igen, mert az arc tetszik a másik embernek. Vannak még más erényei is, de a szellemi tevékenységeket tulajdonképp egyáltalán nem szolgálja olyan erősen, mert ami szellemileg benne rejlik, az mindig az előző földi létbe vezet vissza; a fej az átformált megelőző földi lét. És igazi értelme csak akkor van az ember számára, hogy feje legyen, ha tud valamit az előző földi életeiről.

Az összes többi dolog egyáltalán nem a fejből ered. Valójában ugyanis tudat alatt az ujjaink szerint számolunk. A valóságban 1-től 10-ig az ujjainkon számolunk, majd tovább, 11, 12, 13, 14 a lábujjainkon. Ez ugyan nem látszik, de így teszünk 20-ig. És amit ily módon a testünkben teszünk, az csupán letükröződik a fejben. A fej csupán szemlélője mindezeknek. Az ember feje valójában csak tükre annak, amit a test cselekszik. A test gondolkodik, számol; a fej pusztán külső szemlélő.

Ez a fej különös hasonlóságot mutat valami mással. Ha ez itt egy autó (Steiner rajzol), és mi kényelmesen benne ülünk, akkor semmit sem kell tennünk, a sofőrnek kell dolgoznia, ott elöl. Mi csak bent ülünk, és körülvisznek minket a világban. Így van ez a fejjel is; nem ő erőlködik, csak egyszerűen rajta ül a testen, kényelmesen körbehordoztatja magát a világban, és mindent megszemlél. Amit a szellemi életben teszünk, azt mind a testünkből kiindulva tesszük. A matematika a testből indul ki, a gondolkodás is a testből indul ki, az érzés is a testből indul. A számológép éppen annak a tévedésnek a következménye, miszerint az ember a fejével számol. Akkor aztán a számológéppel tanítják a gyereket számolni, vagyis a fejét erőltetik, és a fej azután tovább erőlteti a testet, hiszen számolnia mégis a testnek kell. Nem veszik figyelembe, hogy a testnek kell számolnia. Ez a fontos. Ezért helyénvaló, hogy az ujjain és a lábujjain számoltassuk a gyermeket, ahogy egyáltalában nagyon jó volna, ha a lehető legügyesebbé igyekeznénk fejleszteni a gyerekeket. Semmi sem jobb például az életre nézve, mintha egészében ügyessé tesszük az embert! Ezt nem lehet a sport által; az nem tesz ügyessé. De az ügyessé tesz például, ha egy irónt fogatunk az ember nagy és a következő lábujja közé, és megtanítjuk írni a lábával, a számjegyeket is leírni lábbal. Ez olyasvalami, ami bizony jelentős lehet, mert a valóságban az ember teljes testét áthatja a lélek és a szellem. A fej a felkapaszkodó és tétlen potyautas, miközben a test mindenben a sofőr; neki kell tennie mindent.

Így kell tehát sokfelől próbálkozva felépítenünk azt, amit a gyermeknek a számolásban meg kell tanulnia. Ezért fontos, hogy miután egy ideig így dolgoztunk, oda is eljussunk, hogy ne csak hozzátevéssel idézzük elő a számolást - sőt, ez a legkevésbé fontos módja a számolásnak -, hanem tanítsuk meg a gyereknek: Itt az egység. Ezt most felosztjuk (lásd az ábrát)*: itt a kettősség.

Nem egy másik egységet tettünk az egyik mellé, hogy kettőt kapjunk, hanem az egységből hoztuk elő a kettősséget. Ez itt az egység (fent), ez pedig most a hármasság. Ily módon elképzelést, képzetet adhatunk arról, hogy az egység tulajdonképpen átfogó, magában foglalja a kettősséget, hármasságot, négyességet. Ha így tanul számolni (lásd a sémát) 1, 2, 3,4 stb., akkor elevenek lesznek a gyermek fogalmai. Ezáltal megtörténik a gyermekben a számok lényegének benső áthatása.

Az ókor egy bizonyos szakaszában egyáltalán nem is ismerték így a mi számlálásfogalmunkat, ahogy mindig csak hozzáteszünk egy következő babszemet a többihez, vagy a számológép egyik golyóját áttoljuk a többi mellé, hanem bizony azt mondták: az egység a legnagyobb; minden kettősség ennek csak a fele, és így tovább. Ily módon behatolunk a számolás lényegébe, szemléletesen, kívülre vetítve. A gyermek gondolkodását mindig csak a külső dolgokon, a szemlélhetőn kell fejlesztenünk, s az absztrakciót lehetőleg tartsuk távol.

A gyermeknek így fokozatosan lehetősége nyílik arra, hogy bizonyos fokig magáévá tegye a számsort, kezdetben például 20-ig, azután 100-ig stb. De ezen a módon kell eljárnunk, hogy elevenen tanítsuk meg a gyermeknek a számolást. Akkor tud majd számlálni a gyerek. Előbb valóban számlálni kell megtanulnia a gyermeknek - külön kiemelem nem pedig rögtön számítani, hanem számlálni. A gyermeknek tudnia kell számlálni, mielőtt elkezdjük a számítási műveleteket.

Ha azután elsajátíttattuk a gyermekkel a számolást, akkor az következik, hogy rátérjünk a műveletekre. A számítási műveleteket is az eleven világból kell levezetnünk. Ami eleven, az mindig egy egész, és előbb mindig egészként adott. Rosszat teszünk az emberrel, ha arra késztetjük, hogy mindig részekből tegyen össze egy egészet, ha nem arra neveljük, hogy az egészre tekintsen, és ezt az egészet bontsa azután részekre. Azáltal, hogy arra ösztönözzük a gyereket, hogy az egészre tekintsen, azt bontsa és ossza fel, ezáltal az eleven élethez vezetjük a gyermeket.

Sok mindent nem veszünk észre abból, amit a materialista kor tett velünk, az emberiség kultúrájával kapcsolatban. Manapság egyáltalán nem rökönyödünk meg azon, hanem magától értetődőnek tekintjük, hogy építőkockákkal játsszanak a gyerekek, amikor is különálló elemekből egy építményt raknak össze. Ez kezdettől fogva eltávolítja a gyermeket az eleven élettől. Lényéből következően a gyereknek egyáltalán nincs igénye arra, hogy részekből egészet rakjon össze. Sok másféle, mindazonáltal számunkra kényelmetlenebb igénye van. A gyermeknek rögtön igénye lesz arra, ha egyszer felfedezte, hogy ha egy órát adunk neki, azt mindjárt szétszedje, az egészet a darabjaira bontsa, ez pedig sokkal inkább megfelel az ember lényének, hogy utánajárjon, hogyan bomlik egy egész a részeire.

Ez az, amit most a számtan tanításánál is figyelembe kell vennünk. Hogy ez az egész kultúránkra befolyással van, azt a következő példából beláthatjuk.

Úgy a X111-X1V. századig egyáltalán nem helyeztek akkora hangsúlyt arra, hogy az emberi gondolkodásban egy egészet a részeiből rakjunk össze. Ez csak később jelent meg. Az építőmester sokkal inkább az egész gondolatából kiindulva építkezett és részékre bontott, mint hogy részekből rakott volna össze egy épületet. A részekből való összeállítás csak később került bele az emberi civilizációba. Ez pedig azután oda vezetett, hogy az emberek egyáltalában mindent a legkisebb részekből összetettnek kezdtek elgondolni. Ebből következett az atom-elmélet a fizikában, amely csakis a nevelésből ered. A mi nagy tudósaink egyáltalán nem beszélnének így ezekről az apró démonkarikatúrákról, az atomokról - hiszen démonok karikatúrái az atomok ha nem szoktunk volna hozzá a nevelés terén, hogy mindent részekből tegyünk össze. Ennek lett a következménye az atomizmus, amelyet manapság kritizálunk; a kritikák azonban meglehetősen feleslegesek, mert az emberek nem tudnak elszakadni attól a fordítva gondolkodástól, amihez négy-öt évszázad óta hozzászoktak: ahelyett, hogy az egészből kiindulva gondolnánk bele a részekbe, a részekből kiindulva gondolunk az egészre.

Olyan dolog ez, amit a számtan tanításánál különösen fel kell idéznünk. Ha a távolból közeledünk egy erdőhöz, akkor előbb az erdőt látjuk, és majd, csak ha közelebb érünk, akkor tagoljuk az erdőt az egyes fáira. Így kell eljárnunk a számtanban is. Soha nem 1, 2, 3, 4, 5 pénzdarab van a tárcánkban, hanem egy kupac pénzérme. Együtt van az az öt. Ez egy egész. Ez van előbb. És ha borsólevest főzünk, akkor sem 1, 2, 3, 4, 5 ... 30-40 borsószemet veszünk, hanem egy marókkal. Egy kosár almában sem 1, 2, 3, 4, 5, 6, 7 stb. almának van, hanem egy kupacnyi alma van a kosarunkban. Egy egész. Először egyáltalán nem érdekel minket, hogy pontosan mennyi is az; van egy kupac almánk (Steiner rajzol). Ezt a kupac almát most hazavisszük. Három gyermek vár otthon. Először egyáltalán nem az a célunk, hogy mindjárt úgy osszuk el az almákat, hogy mindenki ugyanannyit kapjon. Az egyik gyerek talán kicsike, a másik nagy. Belemarkolunk, s a nagyobbik gyereknek egy nagyobb kupacot adunk, a kisebbiknek meg egy kisebbet; így osztjuk a kosámyi almánkat három részre.

Az osztás egyébként is különös történet! Volt egyszer egy anya, aki egy nagy szelet kenyérrel a kezében azt mondta Henrik fiának: „Oszd el ezt most, de keresztény módjára oszd meg...” Azt kérdezte erre Henrik: „Mi az, hogy keresztény módjára megosztani?” „Nos - felelte az anya - egy kisebb és egy nagyobb darabra kell vágnod a kenyérszeletet, s a nagyobbikat Anna nővérednek adod, te pedig megtartod a kisebbiket...” Mire Henrik: „Nem, akkor inkább Anna ossza el keresztény módjára!”

Más fogalmakat is segítségül kell hívnunk. Úgy osztunk például, hogy ennyit adunk az első gyereknek (lásd a határvonalakat az ábrán), a második gyerek ezt a kupacot kapja, a harmadik pedig emezt. Hogy rendesen át tudjuk látni a dolgot, előbb a teljes kupacot számoljuk meg, hiszen számlálni már tud a gyerek. 18 alma van benne. Most pedig megszámoljuk: Hány almát kapott az első gyerek? 5. Hányat a második? 5. Mennyi van a harmadiknak? 8.

Így az egészből indultunk ki, a teljes kupac almából, és felosztottuk három részre.

Igen gyakran úgy tanítják ezt, hogy azt mondjuk: itt van 5, megint 5, meg 8; ezeket összeszámolod, akkor 18-at kapsz. Ekkor a részekből indulnak ki, és az egészhez jutnak. Ez viszont halott fogalmakat ad a gyermeknek, nem pedig eleveneket. Induljunk ki az egészből, a 18-ból, és osszuk fel a tagokra, így jussunk el az összeadáshoz.

Ne úgy tanítsunk tehát, hogy az egyes összeadandókból vagy tagokból indulunk ki, hanem az összegből induljunk - ez az egész - és ezt tagoljuk szét az egyes tagokra. Akkor oda juthatunk, hogy azt mondjuk: de másképp is szétoszthatom ezt. Eloszthatom így ... akkor más tagokat kapok, az egész mindig ugyanaz marad. Azáltal, hogy nem úgy vesszük az összeadást, ahogy azt igen gyakran teszik, hogy előbb az összeadandókat nézik és az után az összeget, hanem előbb az összeget adjuk meg és ez után a tagokat, így egészen eleven, rugalmas fogalmakat kapunk. Arra is rájövünk, hogy ahol maga a szám a lényeg, az egész bizony maradandó; az egyes összeadandók, a tagok, változhatnak. A számfogalomnak ez a sajátossága, hogy a tagokat különbözőképp csoportosítva gondolhatjuk el, igen szépen megmutatkozik ekkor.

Azután tovább léphetünk, és azt mondjuk: ha azonban valami nem csupán csak egy szám, hanem magában hordozza a számot, mint az ember, akkor nem lehet különféleképpen felosztanunk. Ha például az ember törzsét tekintjük, és ami hozzá csatlakozik, a fejet, karokat, lábakat, akkor nem oszthatjuk fel tetszőlegesen az egészet, akkor nem mondhatjuk: az egyik lábat így vágom ki, a kezet meg emígy, stb.; hanem a természet már egy adott módon felosztotta ezt.

Ahol csak számlálásról van szó, ott nincs természettől adott felosztás, ott különbözőképpen tagolhatunk.

Ez az, ami által egyáltalán lehetőséget kapunk, hogy életet és eleven folyást vigyünk a tanításba. Mindenféle pedantéria kipereg, és meglátjuk, hogy olyasvalami kerül be, amit a gyermek különösen jól tud használni: egészséges - nem gyerekes - értelemben vett humor kerül bele a tanításba. A humornak márpedig bele kell kerülnie a tanításba.

Jól értsük ám a „humor” szót; oly gyakran félreértelmezik ezt!

Így kell mindig eljárnunk a tanítás során: mindenütt az egészből kell kiindulnunk. Nézzünk egy életből vett történetet. Az édesanya elküldte Marikát almáért. Marika 25 almát kapott. Ezt a kofaasszony felírta egy cetlire. Marika hazaér és csak 10 almát hoz. A tényállás világos, az életből való: Marika 25 almát kapott, és csak tízet hozott haza. Marika becsületes kislány, tényleg egyetlen almát sem majszolt el hazafelé, de mégis csak 10 almával ért haza. Most valaki jön, aki szintén becsületes, és az összes almát elhozza, amit Marika útközben elveszített. Az most a kérdés: hány almát is hoz ez az ember? Látjuk a távolban, ahogy jön. De szeretnénk előre tudni, hány almát is hoz. Nos, Marika hazaért, 10 almát hozott, 25-öt kapott, látni a cetlin, amire a kofaasszony felírta. Tehát 15 almát veszített el.

Látják, megcsináltuk a számítást. Rendszerint így szokták csinálni: adott valami, amiből ki kell vonni valamit, és valamennyi megmarad. Az életben azonban - meg fogunk győződni erről - sokkal gyakrabban fordul elő, hogy azt tudjuk, mennyit kaptunk eredetileg, és mennyi maradt meg, és azt kell megkeresnünk, hogy mennyi veszett oda. Úgy kell tehát végeznünk a kivonást, hogy eleven legyen, hogy a kisebbítendőből és a maradékból indulunk ki, és a kivonandót keressük; nem a kisebbítendőből és a kivonandóból kiindulva és a maradékot keresve. Az úgy halott. Eleven az, ha a kisebbítendőből és a maradékból indulunk ki, és a kivonandót keressük. Ezáltal életet viszünk a tanításba.

Látjuk, ez életszerű, ha az édesanya és Marika történetét nézzük, és azét, aki a kivonandót utána hozza. Marika a kisebbítendőből elveszítette a kivonandót, ezt pedig úgy akarjuk helyretenni, hogy aki utána jön, akit közeledni látunk, arról tudni akarjuk, mennyit is kell hoznia. Eletet viszünk így az egész kivonásba, valódi életet. Ha csak azt kérdezzük: mennyi marad meg - az csak halott dolgokat visz a gyermek lelkébe. Mindig arra kell gondolnunk, hogy mindenütt eleven, nem pedig halott dogokat vigyünk be a gyermekbe.

És így léphetünk azután tovább. A szorzást úgy csinálhatjuk, hogy azt mondjuk: az egész, a szorzat adott; hogy találhatjuk meg, hányszor van meg valami ebben a szorzatban? Látják, így találunk eleven dolgokra. Gondoljanak csak bele, mennyire halott az, ha azt mondjuk: felosztom ezt az embercsoportot, itt vannak hárman, itt megint hárman, és így tovább; és most azt kérdezem: hányszor hárman vannak összesen? - Ez így halott, ebben nincsen élet.

Ha fordítva járunk el, az egészet vesszük, és azt kérdezzük, hányszor van meg ebben valamilyen csoport, úgy életet vihetünk a dologba. Azt mondhatjuk például a gyerekeknek: látjátok, az osztályunk egy bizonyos számú gyerekből áll. Számoljuk csak meg. 45-en vagytok. - Most kiválasztunk ötöt, 1, 2, 3, 4, 5, őket kiállítjuk. Aztán megszámoltatjuk: hányszor vannak meg ők öten ebben a 45-ben? Látják, így megint az egészre utalok, nem a részletekre. Hány ilyen ötös csoportot csinálhatunk még? Akkor arra jutunk, hogy még nyolc ötös csoport van a maradékban. Fordítva csináljuk tehát a dolgot, az egészből indulunk ki, a szorzatból, és azt keressük, hányszor van meg benne egy tényező. Ezáltal élettel telítjük a számítási műveleteket, és mindenekelőtt az átlátható dolgokból indulunk ki. És ez a lényeg, hogy sohase szakítsuk el a gondolkodást az átlátható dolgoktól, máskülönben korán eléri a gyermeket az intellektualizmus, az absztrakció, és tévútra vezetjük vele a gyermeket. Kiszárítjuk őt, és ráadásul - beszélünk majd még a szellemi-lelki-testi nevelésről - a fizikai test kiszáradását is kitenyésztjük benne: a szklerózist.

Azon is sok múlik, hogy úgy tanítsuk a számolást, ahogy azt itt megfigyelhették, hogy az ember idős korára még rugalmas maradjon, ügyes legyen még. Ha az emberi testen tanítunk számolni, ahogy azt bemutattam, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 és azután tovább a lábujjakon - bizony igen jó volna, ha hozzászoktatnánk a gyerekeket, hogy húszig valóban az ujjaikkal és a lábujjaikkal számoljanak. Ne a számológéppel -, ha ezt tanítjuk a gyerekeknek, akkor látni fogjuk, hogy e gyermeki meditáció által - mert ha az ujjakkal, és a lábujjakkal számolunk, akkor gondolnunk is kell az ujjakra és a lábujjakra, ez pedig a saját testen végzett meditáció, még pedig egészséges meditáció -, így életet viszünk a testbe. Akkor idős korban még ügyesek az ember tagjai; megállják a helyüket, mert az egész testünkön tanultunk számolni. Ha csak a fejével gondolkodik az ember, a végtagjaival és a test többi részével nem gondolkodik, akkor e tagjai később nem is tudnak helytállni, és az ember kösz- vényes lesz.

Hogy hogyan is kell mindent az átlátható dolgokból kiindulva - nem pedig abból, amit ma gyakran „szemléltető oktatásnak” neveznek - megszerveznünk a nevelésben és a tanításban, azt most egy adott példával szeretném szemléltetni önöknek, amely tényleg igen sajátos szerepet játszhat a tanítás során. Pitagorasz tételéről van szó, amit bizonyára mindnyájan ismernek, ha tanítani fognak, és talán át is látták már egy hasonló módon, de mégis beszélnénk ma róla. Nézzék, Pitagorasz tétele olyasvalami, amit a tanítás során valóban egyfajta célként tűzhetünk ki a geometriában. Bizony felépíthetjük úgy a geometriát, hogy azt mondjuk: mindent úgy akarunk megszervezni, hogy Pitagorasz tételében éljen csúcsot, miszerint egy derékszögű háromszög átfogójának négyzete egyenlő a két befogó négyzetének összegével. Valami egészen grandiózus dolog ez, hajói megnézzük.

Egyszer egy hölgynek, aki akkor már idősebb volt, csak mert úgy szerette, geometriát kellett tanítanom. Nem tudom, hogy vajon minden előzményt elfelejtett-e - de valószínűleg nem sokat tanult a leánynevelő intézetekben - mindenesetre semmit sem tudott geometriából. Elkezdtem tehát, és az egészet Pitagorasz tételére hegyeztem ki. Nos, Pitagorasz tétele valóban valami rendkívül frappáns dolgot jelentett a hölgy számára. Az ember csak hozzászokik ehhez a meglepő dologhoz. De, hogy egyszerűen megértsük, hogy ha itt egy derékszögű háromszög (Steiner rajzol)8, akkor a felület, amelyet négyzetként az átfogóra emelünk, egyenlő a befogókra emelt két négyzetfelület összegével (I. ábra).

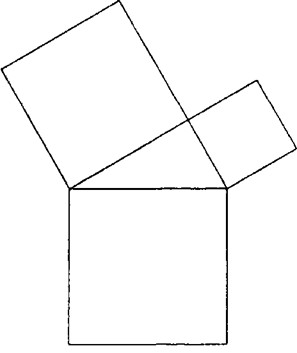
I. ábra

Ha tehát krumplit ültetek, és mindenütt egyenlő távolságra rendezem el a növényeket, akkor, ha ezt és ezt a területet együtt beültetem krumplival, pontosan ugyanannyi krumplit fogok oda ültetni, mint ide, emebbe a földbe. Ez bizony frappáns dolog, egészen meglepő, és ha csak így nézzük, nem láthatjuk át.

És éppen ezt, hogy nem láthatjuk át a dolgot, hogy ez valami elképesztően csodálatos, kellene a lélek belső felizzítására felhasználnunk a tanításban; építenünk kellene arra, hogy itt nem valamiféle teljesen átlátszó dologgal állunk szemben, amit újra és újra be kell vallanunk. Azt mondhatnánk: Pitagorasz tételével az a helyzet, hogy el lehet hinni, de mindig mindjárt el is kell veszítenünk ezt a hitet. Újra és újra át kell gondolnunk, hogy az átfogó négyzete egyenlő a két befogó négyzetének összegével.

Nos, találhatunk mindenféle bizonyítási módokat, s a bizonyítást egészen átlátható módon kellene megadnunk. Könnyű a bizonyítás, ha egyenlőszárú háromszögről van szó. Ha egy egyenlőszárú derékszögű háromszöget tekintünk (Steiner rajzol; II. ábra), akkor ez itt az egyik befogó, itt a másik befogó, ez pedig az átfogó. Amit most narancsszínnel rajzolok fel (1, 2, 3, 4), az az átfogóra emelt négyzet. A (2, 5, 4 6), a két befogóra emelt négyzetek, amit kékkel rajzolok fel.

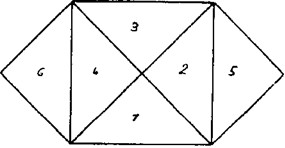
II. ábra

Most megint csak az a helyzet, hogy ha a megfelelő módon e két kék földön (2, 5; 4, 6) krumplit ültetek, ugyanannyi termésem lesz, mint akkor, ha a narancsszínű földön (1, 2, 3,4) ültetek krumplit. A narancsszínű föld az átfogóra emelt négyzet, a két kék föld pedig (2, 5; 4, 6) a két, befogókra emelt négyzet.

Nos, egyszerű a bizonyítás, ha azt mondjuk: a két kék négyzet egy-egy darabja (2, 4) beleesik az átfogó-négyzetbe, már benne vannak. Ezt a darabot (5) feltehetjük ide (3). Ha kivágjuk az egész ábrát, ezt a darabot (6) ráhelyezhetjük erre (1), és máris egyenlő a lefedés. Ekkor tehát egészen átlátható a dolog, ha úgynevezett egyenlőszárú derékszögű háromszöggel dolgozunk. Ha azonban nem egy egyenlőszárú derékszögű háromszöget tekintünk, hanem olyant, amelyiknek minden oldala különböző (mint az I. ábrán), akkor a következőt tehetjük: rajzoljuk le még egyszer ezt a háromszöget (III. ábra: ABC). Most rajzoljuk fel az átfogóra emelt ABDE négyzetet. A következőképpen rajzolhatunk tovább: az eredeti ABC háromszöget átrajzolhatjuk ide (BDF). Azután az ABC háromszöget, illetve a BDF háromszöget, ami ugyanaz, még egyszer berajzolhatjuk ide is (AEG). Ahogy itt még egyszer megvan az eredeti háromszögünk, az egyik (a rövidebbik) befogóra emelt négyzetet berajzolhatjuk így (pirossal): CAGH. Amit tehát pirossal rajzoltam, az az egyik befogó-négyzetünk (CAGH).

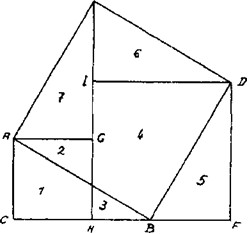
III. ábra

Most pedig, amint látják, ide is berajzolhatom az eredeti háromszögünket (DEI). Itt is megvan. Amit pedig zölddel rajzolok be, az a másik (a hosszabbik) befogóra emelt négyzet (DIHF); és akkor megvan mind a kettő, az egyik befogó-négyzet, és a másik befogónégyzet is. Az egyikhez ezt az AG befogót használtuk, a másikhoz pedig ezt a Dl befogót. Az egyik háromszög itt van (AEG), a másik itt (DEI); de egybevágóak (vagyis kongruensek). Hol van az átfogóra emelt négyzetünk? Ezt most lilával rajzolom át, hogy jól el tudjuk különíteni: ABDE. Itt van tehát az átfogó-négyzet. Most pedig meg kell mutatnunk az ábrán, hogy a piros (1, 2) és a zöld (3,4, 5) terület együtt a lilát (2,4, 6, 7) adja ki.

Azt könnyen beláthatjuk: előbb ezt a piros négyzetet (1, 2) vesszük; ami a két négyzetben közös (2), az, fedésben van. Beleesik ide még a zöld négyzet egyik darabja is (4). Itt van tehát ez a darab (2, 4), amit láthatunk a rajzon, és ami nem más, mint a lila ABDE négyzet egy darabja, valóban egy darab a lila négyzetből. A lila ABDE négyzet tartalmazza a piros négyzet egyik darabját (2); ebből már csak ez a szelet marad ki (1), az még nincsen benne. De ezen kívül benne van a nagy figurában a zöld négyzet egyik darabja is (4). Most már csak arra kell rájönnünk, hogyan helyezzük el, ami még kimaradt (1, 3, 5).

Azt kell látnunk: maradt egy darabunk a piros négyzetből (1), itt egy darabka a zöld négyzetből (3), és kimaradt még ez az egész háromszög is (5), ami szintén a zöld DIHF négyzethez tartozik. Akkor hát fogjuk ezt, ami itt van, ami itt kimaradt, és áthelyezzük amoda; ami tehát emitt kimaradt (5), azt áttesszük ide fel (6). Most itt vannak még ezek a szeletek (1, 3). Ha kivágjuk őket, valóban rájövünk, hogy ez a két felület (1, 3) együtt egybevág ezzel a felülettel (7). Természetesen még világosabban is fel lehet rajzolni, de úgy gondolom, hogy átláttuk a dolgot. Most még csak az a lényeg, hogy azzal, amit mondunk, még közelebb vigyük ezt. Ily módon, egyszerűen a felületek egymásra helyezésével megmutattuk, hogy Pitagorasz tétele helyes. Ha ezeknek a felületeknek egymásra helyezését nézzük, akkor ebben van valami. Ugyan látjuk, ha kivágjuk a dolgot, nem pedig csak felrajzoljuk, hogy igen könnyen átlátható; és mégis, ha később gondolkodunk róla, megint kiesünk a képből. Mindig újra és újra meg kell keresnünk, hogy is van ez. Nem tudjuk elég jól megtartani az emlékezetünkben, ezért újra és újra meg kell keresnünk. És ez jól van így. Bizony nagyon jól van így. Illik Pitagorasz tételéhez. Újra és újra rá kell jönnünk. Azt, hogy beláttuk, újra és újra el kell felejtenünk. Ez illik ahhoz a frappáns minőséghez, ami Pitagorasz tételének sajátja. Ezáltal elevenséget találunk a dologban. Látni fogjuk, ha újra és újra megcsináltatjuk ezt a diákjainkkal, hogy bizony végig kell szenvedniük. Nem jönnek rá megint azonnal, minden egyes alkalommal végig kell gondolniuk. Ez azonban illik Pitagorasz tételének belső elevenségéhez. Az egyáltalán nem jó, ha úgy bizonyítjuk Pitagorasz tételét, hogy simán, filiszter módjára belátható legyen; sokkal jobb, ha újra és újra elfelejtjük, és mindig újként kell megkeresnünk. Ez illik ahhoz a frappáns, olyan különös, meglepetéshez, hogy az átfogó négyzete egyenlő a két befogó négyzeteinek összegével.

Tizenegy-tizenkét éves gyerekekkel igen jól eljuthatunk oda a geometriában, hogy egy ilyesféle felület-összehasonlítással magyarázzuk el Pitagorasz tételét; a gyerekek fantasztikusan fognak örülni, ha belátják, és fellelkesednek rajta. Örömet szerzett nekik a dolog. Most újra és újra meg akarják csinálni, különösen, ha kivágatjuk velük a figurát. Csupán néhány intellektualista semmirevaló diák akad, aki igen jól megjegyzi a dolgot, aki újra és újra össze tudja rakni. A legtöbb - értelmes - gyerek újra és újra elszakad tőle, és végig kell szenvedniük, mire ismét kitalálják, hogy is kell lennie. Ez azonban illik Pitagorasz tételének csodálatosságához, és nem szabad kiszakadnunk ebből a csodálatosságból, hanem meg kell maradnunk benne.