U. levezeti a zenetanítás vezérelveit az első és második iskolaév számára.

Rudolf Steiner: Nem szabadna elmulasztanunk, hogy az objektív, az embertől elkülönített hangot, a hangszerek hangját is meghallgattassuk. Mindig oda kell figyelnünk arra, hogy a gyermek még viszonylag jóval a kilencedik életéve előtt, a második iskolaév második felében, ismerkedjen meg valamilyen szólóhangszerrel, s így később a zongora következne azok számára, akik e téren számításba jönnek. Ez a lényeg, ugye, hogy jól indítsunk ezen a területen.

T. előadja a kamatszámítás folytatását, áttéréssel a betűkkel való számoláshoz. Ha V = végösszeg, T = kiinduló tőke, K = kamat, Sz = százalék, I = idő:

akkor V = T + K. Ebből K = T • Sz • I / 100, és így V = T + (T • Sz • I) / 100

Rudolf Steiner: Ebben a formában ugyebár nem lehet ma tőkét gyarapítani. Ennek a formának csak akkor van realitásértéke, ha I egyenlő vagy kisebb, mint egy év. Hiszen a valóságban két eset lehetséges: vagy évente leemelik a kamatokat, akkor mindig az azonos kiinduló tőke marad meg; vagy meghagyják a kamatokat a tőkénél, s akkor kamatos kamat számítására van szükség. Ha elhagyjuk az I időt, vagyis egy évre számolunk, úgy reális a dolog. A realitást kell mutatnunk a gyerekeknek.

Jó lesz, ha szigorúan dolgozunk azon, hogy az áttérés a betűkkel való számolásra valóban meg is történjék. Előbb az összeadástól a szorzásig vezetjük le az átmenetet, azután a kivonástól az osztásig.

Rudolf Steiner a következő példán magyarázza el az átmenetet a számjegyekkel való számolástól a betűkkel való számolás- hoz. Először is felírunk egy olyan számösszeget, melyben az összeadandók mind különbözőek:

20 = 7 + 5 + 6 + 2

Egyes összeadandók azonosak is lehetnek:

25 = 5 + 5 + 9 + 6

És minden összeadandó is lehet azonos:

18 = 6 + 6 + 6

Ha most a tegnap már leírt módon áttérünk arra, hogy a számokat betűkkel helyettesítjük, akkor ebből először is a következő összegem van:

S₁ = a + a + a,

ez három a, háromszor a = 3 • a; azután folytatva:

S₂ = a + a + a + a + a,

ötször a = 5 • a; azután:

S₃ = a + a + a + a+ a + a + a,

hétszer a = 7 • a és így tovább. Tovább folytatom, vehetem kilencszer, huszonegyszer, huszonötször. Azután m-szer veszem:

S_m = a + a + a + a + a... m-szer = m • a.

Így megkapom az azonos összeadandók számának meghatározatlanságából az egyik szorzandó elemet, miközben maga az adott összeadandó a másik szorzandó elem. Ily módon az összeadásból a szorzás könnyen levezethető és megértethető. Így hajtjuk végre az átmenetet a meghatározott számjegyektől az algebrai kifejezésekhez, mint: a • a = a2; a • a • a = a3. Ugyanígy vezethetjük le a kivonásból az osztást.

Ha kivonjuk b számot egy nagyon nagy a számból, akkor M, maradékot kapunk:

M1 = a - b

Ha megint elvesszük belőle b értékét, akkor az M2 maradékot kapjuk meg:

M2 = a - b - b = a - 2 • b

b harmadszori elvétele a következőt adja ki:

M3 = a - b - b - b = a - 3 • b

és így tovább. Addig folytathatjuk ezt, amíg az a számból nem marad több maradék, ehhez n-szer végezzük el:

M = a - b - b - b - b ... n-szer = a - n • b.

Ha azután nem marad maradék, vagyis az utolsó maradék = 0, akkor:

0 = a - n • b.

Ekkor teljesen felosztottuk a-t, hiszen ugye nincs maradék: a = n • b. 

n-szer vettem el b-t; a-t csupa b-re osztottam fel:

a / b = n,

ekkor ugye teljesen elfogyasztottuk a-t. Úgy találtam, hogy n-szer végezhetem el ezt, és ezzel áttértem a kivonásról az osztásra.

Azt mondhatjuk tehát: a szorzás az összeadásnak egy sajátos esete, az osztás pedig a kivonás sajátos esete, amikor is ugye nem csupán egyszer, hanem ismételten adunk hozzá illetve veszünk el.

A negatív és az imaginárius számokra terelődik a szó.

Rudolf Steiner: Egy negatív szám az egy kivonandó, amelyhez nincs jelen kisebbítendő; felszólítás egy művelet végrehajtására, amelyhez nincs anyag, amelyet nem lehet végrehajtani. - Eugen Dühring értelmetlenségnek tartván elutasította az imaginárius számokat[1] és azt mondta Gauss imagináriusdefiníciójáról, hogy az szamárság, nem realitás, kiokoskodott dolog.

Tehát a szorzást mindig az összeadásból vezetjük le, és azután a hatványozást a szorzásból. És tovább, az osztást a kivonásból, a gyökvonást az osztásból.

összeadás	kivonás
szorzás	osztás
hatványozás	gyökvonás

Majd csak a betűkkel való számolás bevezetése után, a 11-12 életévtől kezdve térünk rá a hatványozásra és a gyökvonásra, mert ugye a gyökvonásban egy többtényezős algebrai kifejezés hatványozása szerepel.

Ebben az összefüggésben át kell még vennünk: a bruttó illetve nettó érték kiszámítását, a csomag- és göngyöleg-számítást.

Valaki kérdést tesz fel a képletek használatára vonatkozóan.

Rudolf Steiner: Most viszont arról van szó, hogy vajon inkább nem használná olyan gyakran a képletet, hanem újra és újra végigvinné a gondolatmenetet - miközben ugye kétségtelenül gyakorolhatja a beszédkultúrát, ez bizony helyénvaló -, vagy pedig hogy nem akar-e mégis áttérni a képlet használatára. Ha tapintatosan éri el, hogy jól megértsék a képletet, az is igen hasznos, ha bizonyos mértékig beszédkultúrát gyakorlunk rajta.

De egy bizonyos pont után az is jó, ha a képletet valamiféle megérzéssé tesszük a gyermekben. Olyasvalamivé tesszük a képletet, aminek benső élete van, így például ha ebben a

K = T • Sz • I / 100

esetben I értéke nő, akkor a gyermek érezze meg az egész kifejezés értékének a növekedését.

Ezzel tehát el is hangzott volna, amit ehelyütt el akartam mondani, hogy konkrét számokat kellene használnunk az ilyen alkalmakkor, mint a kamat- illetve a százalékszámítás, hogy átmenetet találjunk a betűkkel való számoláshoz, azon keresztül pedig levezessük a szorzást, az osztást, a hatványozást, a gyökvonást. Ezek ugye olyan dolgok, amelyeket mindenképpen el kell végeznünk a gyerekekkel.

Most azt a kérdést szeretném felvetni: Jónak tartják-e már akkor foglalkozni a hatványozással és a négyzetgyökvonással, a gyökvonással, még mielőtt a betűkkel való számolást gyakorolták volna, vagy pedig utána foglalkoznának vele?

T.: A hatványozással előtte, a gyökvonással utána.

Rudolf Steiner: Tehát ön mégiscsak abból indul ki, s a jövőben is ebből kellene kiindulnia, hogy lehetőleg hamar, a 11-12 életévtől kezdve bevezeti a betűkkel való számolást és csak ez után tér rá a hatványozásra illetve a gyökvonásra. Hiszen a betűkkel való számolás ismeretében igen egyszerű és gazdaságos módon lehet négyzetre emelni, köbre emelni, hatványozni és gyököt vonni a gyerekekkel, miközben ez előtt rettenetesen sok időt kellene ráfordítani. Könnyen és gazdaságosan fogják tudni tanítani ezeket a dolgokat, ha legelőször is megbeszélték a gyerekekkel a betűkkel való számolást.

E. bemutatja kidolgozott történelmi témáját a legfelsőbb osztály diákjai számára a városok alapításáról illetve fejlődéséről, és a magyarok portyázásainak idejére vonatkoztatva „Németország”-ról beszél.

Rudolf Steiner: Én bizony nagyon odafigyelnék rá, nehogy akaratlanul is zavaros elképzelések keletkezzenek. Természetesen akkoriban, Henrik, az úgynevezett városépítő idejében, Németország még nem létezett. Valahogy így kell kifejeznünk magunkat: városok a Rajna vagy a Duna mentén, amelyek később németté váltak. Nemde bár, a 10. század előtt ugye nem is a magyarokkal volt dolgunk; korábban az ilyen betörések alkalmával hunokkal illetve avarokkal volt dolgunk. A 10. századtól kezdve azután már mondhatjuk, hogy „Németország”.

Látják, én például megpróbálnék ilyenkor - ez ugye olyan feladat, amelyet a népiskolák legfelsőbb osztályainak diákjaival szokás elővenni - megtanítani a gyerekeknek egyféle kronológiafogalmat. Ha csak úgy „9-10. század”-ról beszélünk nekik, akkor túl kevéssé lesz konkrét az elképzelésük. Hogyan érnék el, hogy konkrét elképzelés alakuljon ki a gyerekekben az időről?

Világossá tehetnék a gyermeknek: „Mikor te most ennyi idős vagy, hány éves az édesanyád, az édesapád? Azután mennyi idős a nagypapa, a nagymama?” - Előveszik az egymásra következő generációkat, s így világossá tehetik a gyermek előtt, hogy egy ilyen generációhármas körülbelül száz évet ölel fel. Tehát száz évre három generáció esne. Száz évvel ezelőtt tehát gyerekek voltak a dédszülők. Kilenc évszázaddal ezelőtt nem három, hanem 9 • 3 = 27 generációval jártunk korábban. - „Képzeld csak el”, mondjuk a gyereknek, „hogy fognád az apád kezét, aki a nagyapád kezét fogja, ő a dédapádét és így tovább. Ha így egymás mellett állnátok, hányadik lenne a sorban 1. Henrik, hányadik ember nézne szembe a magyarokkal úgy a 926. év táján? A huszonhetedik ember lenne az.” - Az eseményeket azután igen szemléletesen ábrázolnám. Miután eljuttattam így a gyerekeket a konkrét elképzeléshez, hogy milyen régen is volt ez, leírnám nekik akkor a magyarok hadjáratait. Megvilágítanám nekik, hogyan rohanták meg annak idején a magyarok Közép-Európát. Hogyan is törtek be a magyarok olyan vadul, hogy mindenkinek menekülnie kellett, még a bölcsőben fekvő kisdedeknek is, akiket fel kellett vinni a hegyek ormaira. Azután hogyan égettek fel falvakat és erdőket a betörő magyarok. Igen szemléletesen írnám le a magyarok rohamát.

E. tovább ecseteli, hogyan határozta el Henrik, abból a felismerésből kiindulva, hogy a megerősített Goslarban képes volt ellenállni a magyaroknak, megerősített városok alapítását, s hogy ily módon számos városalapításra került sor.

Rudolf Steiner: Nem tudná ezt a leírást még egyszer, kultúrtörténeti szempontból előadni? Hiszen az amolyan monarchikusan feltupírozott történelmi legenda, hogy Henrik alapította volna ezeket a városokat. Mindezek a 10. századi városok az alapjaikban, a vásártereikben ugyebár már megvoltak. Csupán elősegítették a kiépülésüket azáltal, hogy az ezen városok környékén élő emberek becsatlakoztak, hogy így egy könnyebb védekezési lehetőséget nyerjenek a rájuk törő magyarokkal szemben, és így megerősítették ezeket a helyeket. Inkább gazdasági okok voltak azok, amelyek közreműködtek, és amelyek a városok kialakulásához vezettek. Henrik ehhez nem sokat tett hozzá.

Arra kérném csak önöket, hogy igen szemléletesen adják le mindezt, eljárásuk életteli legyen, hogy a gyerekek szemléletes belső képeket kapjanak, hogy így mindent valóságosan megragadhassanak. Működtetniük kell a gyerekek fantáziáját, és olyan eljárásokat kell használniuk, amint az idő konkretizálásánál megmutattam önöknek. Tényleg nem érünk azzal semmit, ha tudjuk, hogy melyik évben volt például a Zama melletti csata és így tovább, de akkor igen, ha elképzeljük, ha tudjuk, hogy Nagy Károly a harmincadik volna az őseink sorában, ha a generációk kézen fognák egymást, s ez által akkor szemléletes, konkrét elképzelést kapunk az időről. Akkor sokkal közelebb kerül hozzánk ez a korszak - még szép, hogy sokkal közelebb kerül! -, ha tudjuk, hogy Nagy Károly a harmincadik generációs őseink sorában keresendő.

T.: Nem volna jó az ilyen kulturális szemléletű leírásoknál utalni az akkori korok emberének teljesen másféle gondolkodására és érzésvilágára?

Rudolf Steiner: Bizony, erre ugyebár mindig utaltam az előadásaimban és másutt is. Mindenek előtt arra, hogy nevezetesen a 15. századi nagy fordulatot, az ez előtti illetve az ez utáni emberek teljesen más megérzéseit, érzésvilágát és gondolkodását igen szemléletessé kell tenniük. Például már Lamprecht is,[2] akit azonban nem szeretnék ezzel különösebben ajánlani, arra törekszik, hogy konstatálja az e korszak előtti emberek teljesen más gondolkodását, megérzéseit és érzésvilágát. - Erre kiélezve még egyáltalán nem is használták a dokumentumokat.

Ha egy kicsit bele szeretnének merülni a kultúrtörténeti szemléletmódba, akkor mindenek előtt ki kell tudniuk fejleszteni egy bizonyos szimatot, és ha rendelkeznek ezzel a tágabb és szűkebb dolgok iránt, amikről a szerzők mesélnek, a korlátok között mozgó illetve a valamivel nagyvonalúbb leírások iránt, akkor helyénvalóbb elképzeléseket nyerhetnek kultúrtörténeti dolgokkal kapcsolatban.

Rudolf Steiner egy rákérdezésre reagálva a következő művek beszerzését ajánlja a tanári könyvtár számára:

Buckle,[3] A civilizáció története Angliában.

Lecky,[4] Az európai felvilágosodás története.

Ezeken iskolázhatjuk a kultúrtörténeti szemléletmód metodikáját. Lamprechttől a régebbi írásai jöhetnének számításba, de sok minden téves és szubjektív nála.

Ha nem sajátították el a valódi kultúrtörténeti hajtóerők megérzésének ösztönét, akkor fennáll annak a veszélye, hogy igazi Wildenbruch[5]-féle blődséggel, Wildenbruch-féle dilettantizmussal például a császár- és királydrámákat, és az olyan családi perpatvarokat, mint amilyenek Jámbor Lajos és fiai között dúltak, lényeges kultúrtörténeti eseményeknek tartsák.

Gustav Freytag[6] „Képek a németek múltjából” című műve egészen jó, de nem szabad, hogy hagyjuk magunkat lekenyerezni e nagymamák számára íródott történelemszemléltetés kedélyessége által. Éppen manapság lényeges, hogy elhagyjuk azt a gondolkodás- és érzületbeli stílust, mely a 19. század közepének változás szelét hirdető irodalmának („Grenzbotenliteratur”) alkotóira volt így jellemző, Gustav Freytagra, Julian Schmidtre[7] és így tovább. Őt Lasalle[8] „Schmulian Jüd”-nek hívta (kb. „érzelgős zsidó”); Lasalle-tól ennek nem volt antiszemita hangzása.

Houston Stewart Chamberlain „A XIX. század alapletéteményei” című művére kérdeznek rá.

Rudolf Steiner: Chamberlainnél[9] is igencsak jó ösztön kialakítására van szükségünk, mert nála az anyag egynegyed része szellemes, háromnegyede pedig sivár, egészségtelen holmi. Nagyon sok nagyon jó dolog szerepel nála, de mindent önmagunknak kell átnéznünk és mi magunknak kell ítéletet alkotnunk. A kultúrtörténeti ábrázolások jobbak Buckle-nál illetve Lecky-nél. Chamberlain inkább egy amolyan szmokingot viselő úr. Kissé hiú úriember ugyebár, akinek nem kell éppen tekintélynek számítania, akinek azonban mégiscsak volt néhány jó megjegyzése. Nem is végezte valami szépen, ugye - a „Frankfurter Zeitung” című lappal folytatott perére gondolok.

Kautsky[10] írásait említik meg.

Rudolf Steiner: Igen, ha szabályosan az ellenkezőjét fogadjuk el annak, amit ő itt állít. A modern szocialistáktól jó és érdekes tényanyagot kaphatunk, ha nem hagyjuk magunkat elkábítani az elméletek által, amelyek áthatják az ábrázolásaikat.

Mehring[11] is sajátos képet kínál, amint előbb a szociáldemokrácia történetéről írott könyvében a szociáldemokratákat szidja, amíg ő maga szabadelvű; majd azután, mikor átáll a szociáldemokratákhoz, csupán átruházza a szidalmat a szabadelvűekre.

M. bevezetést ad a matematikai földrajz alapfogalmaiba a tizenhárom éves diákok számára, a napfelkelte illetve a nappálya megfigyeléseiről.

Rudolf Steiner: Ha kivitték a gyerekeket a szabadba, akkor ezt az élményt később nagyon jól tudják majd rajzzá alakíttatni velük, miközben odafigyelnek, hogy legyen egy bizonyos párhuzam a rajz és a között, amit a gyerekek a szabadban láttak. Tanácsos viszont, hogy ne adjunk egyszerre túl sokat az ilyen vonaljellegű dolgokból. Nagyon fontos, hogy megtanítsuk a gyerekeknek ezeket a dolgokat, de ha túl sokat fogunk egybe, akkor oda jutunk, hogy a gyerekek nem bírják már felfogni. Beilleszthetjük a földrajzba és a geometriába. Az ilyen feldolgozások körülbelüli lezárása az volna, hogy levezetjük az ekliptika (nappálya) és a koordináták fogalmát.

A. ugyanazt a témát, a napfelkeltét és naplementét fejti ki kisebb gyerekek számára, és megpróbálja egy sematikus rajz segítségével világossá tenni a nap és a bolygók járását.

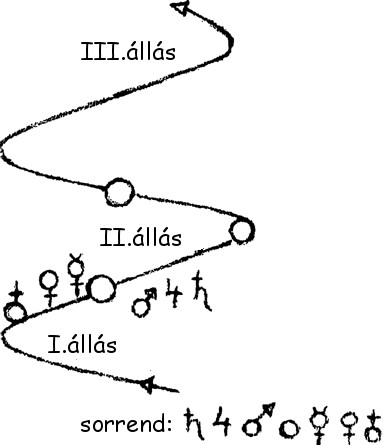
Rudolf Steiner: Nos, ez a fölfogás egyre inkább veszíteni fog a jelentőségéből, mert az azóta ezekkel a mozgásokkal kapcsolatosan feltételezett dolgok nem teljesen helytállóak. Valójában ilyen mozgással[12] van dolgunk (Rudolf Steiner a táblára rajzol):

Ekkor például (I. állás) egyszer itt van a Nap; itt a Szaturnusz, a Jupiter, a Mars, és itt a Vénusz, a Merkúr, a Föld. Nos, ezek mind úgy haladnak egymás után a megadott irányban (csavarvonalban), hogy amikor azután a Nap átér ide (II. állás), akkor a Szaturnusz, a Jupiter és a Mars itt vannak, a Vénusz, a Merkúr és a Föld pedig emitt. S most a Nap még tovább fordul és ide ér (III. állás). Ezáltal keletkezik az a látszat, mintha a Föld a Nap körül keringene. A valóságban a Nap elöl jár, s a Föld mindig utána kullog.

B. bemutat valamit az óegyiptomi kultúrából.

Rudolf Steiner: Mindenekelőtt arra kellene rátérnünk, hogy bemutassuk, milyen is az ábrázolásuk teljesen eltérő alapelve. A régi egyiptomiaknál fennáll az a hiányosság, hogy perspektíva nélkül szemlélődnek. A régi egyiptomi profilból festi le az arcot, a test többi részét pedig szemből. A látásmódnak ezt a sajátosságát mindenképpen közvetítenünk kell a gyermekeknek.

Azután kapcsolatba kellene hoznunk az egyiptomi rajzolást és festészetet a természetrajzi elvvel, amelyet gyakoroltak, hogy állatfejjel ábrázoltak embereket és így tovább. Már a legrégebbi időkben is egészen messzemenően művelték az ember állatokhoz hasonlítását. Azután megtaníthatnánk a gyerekeknek, mi is hajlamosít erre minden emberi fejformában, amit részben ma is láthatnak még a gyerekek.[13] Az egyiptomiak még érzékelték ezt a rokonságot az emberi fiziognómia és az állatok között. Ők a látásmódnak még ezen a gyermeki szintjén álltak.

B. a piramisok tárgyalásánál megkérdezi, mit is kellene tulajdonképpen elmondani róluk a gyerekeknek.

Rudolf Steiner: Természetesen rendkívül fontos, hogy fokozatosan megpróbáljuk a gyerekeknél is a jóra kicserélni a hibás elképzelést. A piramisok valójában ugye beavatási helyek voltak. S ekkor eljutunk oda, hogy fogalmat adjunk a gyerekeknek a magasabb egyiptomi oktatásról, mely egyúttal beavatást jelentett. Mesélnünk kell valamit arról, mi is történt ott. Vallási szertartásokat végeztek, ahogy ma is végeznek ilyeneket a templomokban, amazok azonban egyúttal oda vezettek, hogy fel tudták ismerni a világmindenséget. A régi egyiptomi ember tehát úgy tanult, hogy ünnepélyes szertartások keretében megmutatták neki, mi történik a világmindenségben és az emberiség fejlődésében. A vallás gyakorlása egy volt az oktatással. Úgy volt, hogy az oktatás és a vallás gyakorlása tulajdonképpen egybeestek.

B. leírja a piramisokon és az obeliszkeken végzett munkát, és azt mondja, hogy azt kell feltételeznünk, hogy a hatalmas kőtömbök szállításához, megmunkálásához és beépítéséhez emberek millióira kellett, hogy szükség legyen. Fel kell tennünk önmagunknak a kérdést, hogyan is lehetett egyáltalán lehetséges az akkori technikai segédeszközökkel megmozgatni és egymásra helyezni a hatalmas, nehéz mészkő - és gránittömböket.

Rudolf Steiner: Igen, de igazán helyénvaló elképzeléseket csak úgy fognak tudni előidézni a gyerekekben, ha megmondják nekik, hogy ha az emberek a mai testi erejükkel dolgoznának, akkor két és félszer annyi emberre lenne szükség. De a valóságban ugye az egyiptomiak két és félszer akkora testi erővel rendelkeztek, mint a mai emberek, legalábbis azok, akik a piramisokon stb. dolgoztak. Természetesen voltak közöttük gyengébb emberek is.

B. megkérdezi, hogy a mitológiával is kell-e foglalkozni.

Rudolf Steiner: Ha ugye nem tudjuk bemutatni az egyiptomi mitológiát a valódi formájában, akkor inkább el kell hagynunk. Ha viszont képesek vagyunk arra, hogy a valódi formájában mutassuk be az egyiptomi mitológiát, akkor azt meg kell tennünk. A Waldorf-iskolában különösen jó volna az egyiptomi mitológia helyes fogalmait, amelyeket önök ugye egészen jól ismernek, már a gyerekeknek is megtanítani, ha egyáltalán foglalkozni kívánunk ezzel.

K. a következő fogalmak kidolgozásáról beszél[14] geometriai hely, kör, ellipszis, hiperbola, lemniszkáta. (Ezt a következő napon még folytatni fogják.)